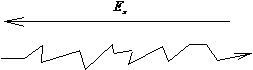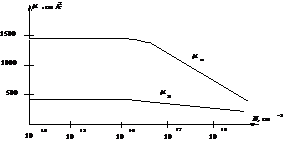1

17. Движение носителей заряда в полупроводниках (дрейф, диффузия).

В соответствии с зонной моделью в полупроводнике имеются два вида подвижных носителей заряда: электроны в зоне проводимости и дырки в валентной зоне. Они могут двигаться под действием температуры (тепловое движение), электрического поля (дрейф) и градиента концентрации (диффузия).

Можно представить, что свободные электроны движутся хаотически через кристаллическую решетку в различных направлениях, сталкиваясь друг с другом и с узлами решетки. При тепловом движении при отсутствии градиента температуры движение системы электронов полностью беспорядочно, так что результирующий ток в любом направлении равен нулю. Столкновения с узлами решетки приводят к обмену энергией между электронами и атомными ядрами, образующими решетку. Воздействие решетки на движение электронов в первом приближении было учтено ранее путем введения эффективной массы. Далее будет более подробно рассмотрено влияние узлов решетки на движение носителей заряда в полупроводнике.

1.5.1. Дрейф свободных носителей заряда. Дрейфом называют направленное движение носителей заряда под действием электрического поля.

Если к полупроводниковому кристаллу приложить слабое электрическое поле , то в течение промежутка времени между столкновениями скорости электронов будут увеличиваться вдоль направления поля (рис. 1.13).

Рис.1.13. Движение электронов в полупроводнике под воздействием внешнего электрического поля

Отметим, что составляющая скорости, обусловленная полем, представляет собой небольшое возмущение хаотической тепловой скорости . Равноускоренное движение под действием поля возможно только в коротких интервалах между столкновениями на длине свободного пробега.

Результирующая скорость носителей в направлении приложенного электрического поля называется дрейфовой скоростью , которая пропорциональна напряженности поля

. (1.35)

Коэффициент в формуле (1.35) называется подвижностью электронов. Подвижность описывает степень влияния электрического на движение электрона и равна

, (1.36)

где - средний интервал времени движения электрона между столкновениями.

Из уравнения (1.1) можно определить плотность тока , протекающего в направлении приложенного электрического поля, если просуммировать произведение заряда электронов на их дрейфовую скорость по всем электронам в единице объема - n:

. (1.37)

Совершенно аналогичные рассуждения применимы и к дыркам. Подвижность дырок обозначается и равна

. (1.38)

Полная плотность тока дрейфа может быть записана в виде суммы электронной и дырочной составляющих:

(1.39)

Член в скобках в уравнении (1.39) определяется как удельная проводимость полупроводника , т. е.

. (1.40)

В примесных полупроводниках обычно основную роль играет только одно из слагаемых формулы (1.40), так как разница концентраций двух типов подвижных носителей заряда в них очень велика.

Поскольку удельное сопротивление есть величина, обратная удельной проводимости, то

. (1.41)

Зависимость удельного сопротивления кремния при комнатной температуре от концентраций примесей доноров или акцепторов приведена на рис.1.14. График построен на основе большого числа измерений удельного сопротивления образцов кремния, содержащих примеси. Этот график широко используется в полупроводниковой промышленности.

Рис.1.14. Зависимость удельного сопротивления кремния от концентрации примеси при температуре 300 К

1.5.3. Диффузия свободных носителей заряда. Рассмотрим еще один вид движения свободных носителей заряда, который возникает под действием градиента концентраций. Такое движение называется диффузией, а ток созданный диффузией носителей заряда называют диффузионным током. В металлах вследствие их высокой проводимости диффузионный ток не играет заметной роли. В полупроводниках же с их более низкой проводимостью и возможностью неоднородного распределения концентраций примесей диффузионный ток играет существенную роль и составляет значительную долю в общем токе.

Наиболее часто в полупроводниках диффузионный ток возникает из-за различия концентраций на отдельных участках. Рассмотрим электронный полупроводник, состоящий из двух участков с различной концентрацией электронов. Предположим, что полупроводник находится в равновесии, т . е . отсутствуют внешнее электрическое поле и перепад температур. Очевидно, что на границе участков возникает градиент концентраций, под действием которого электроны начинают диффундировать из участка с избыточной концентрацией в участок с меньшей концентрацией. Плотность тока диффузии в соответствии с первым законом Фика будет пропорциональна градиенту концентрации

(1.43)

где - коэффициент диффузии электронов;

- градиент концентраций электронов в направлении оси х.

Первый знак "минус" в формуле (1.43) указывает, что ток диффузии направлен в сторону убывания концентрации электронов. Коэффициент диффузии электронов связан с их подвижностью формулой Эйнштейна

(1.44)

Для дырок плотность тока диффузии и коэффициент диффузии соответственно равны

(1.45)

. (1.46)

Знак "минус" в выражении (1.45) появляется из-за положительного заряда дырок.

Следует отметить отличие диффузии заряженных частиц от диффузии нейтральных частиц. Так диффузия нейтральных частиц продолжается до полного выравнивания концентраций во всем объеме. Диффузия же заряженных частиц протекает несколько иначе, поскольку диффундирующие частицы переносят заряд. В результате, внутри полупроводника около границ участков с различной концентрацией нарушается электрическая нейтральность и возникает внутреннее электрическое поле, препятствующее дальнейшей диффузии. Возникающие в результате диффузии внутренние электрические поля играют существенную роль в работе твердотельных приборов. Эти поля будут подробнее рассмотрены в главе 2.

Помимо описанной выше диффузии носителей заряда, возникающей из-за градиента концентраций, в полупроводниках возможна диффузия из-за различия энергий носителей заряда. Так например, локальное нагревание участка полупроводника может вызвать диффузию носителей из участка с более высокой температурой в участок с более низкой температурой.

1.5.4. Полный ток в полупроводниках. В общем случае направленное движение электронов и дырок в полупроводниках обусловлено двумя процессами: дрейфом под действием электрического поля и диффузией под действием градиента концентраций. Поэтому полная плотность тока в полупроводниках содержит четыре составляющих:

, (1.47)

где индексы dr и dif относятся соответственно к дрейфовым и диффузионным составляющим плотности тока.

В одномерном случае, когда движение носителей заряда происходит только вдоль оси х, составляющие плотности тока описываются формулами (1.39), (1.43), (1.45). Для наглядности приведем эти формулы.

Дрейфовые составляющие плотности тока

, (1.48)

. (1.49)

Диффузионные составляющие плотности тока

, (1.50)

. (1.51)

Полупроводник, в котором протекает ток, находится в неравновесном состоянии, поэтому для описания процессов в нем можно использовать квазиуровни Ферми (1.29) и (1.30). Применение квазиуровней Ферми позволяет упростить выражения для составляющих плотности тока. Так электронная составляющая плотности тока, представляющая собой сумму дрейфовой и диффузионной составляющих, определяется через квазиуровни Ферми следующим образом:

. (1.52)

Аналогично для дырок

. (1.53)

Формулы (1.52) и (1.53) показывают, что полная плотность тока для каждого типа свободных носителей заряда пропорциональна градиенту квазиуровня Ферми соответствующего типа носителей вдоль оси х. Это компактное написание может быть очень удобным при использовании энергетических зонных диаграмм для описания полного тока в твердотельном приборе.

В заключение следует отметить, что обычно в полупроводнике превалирует какая-нибудь одна составляющая тока, поэтому выражение (1.47) используется достаточно редко.